08 July 2016
In previous eUpdates: Price Scoring - Getting it wrong? / Price Scoring, Fair Work Practices...and the Living Wage, I discuss relative and absolute price scoring formulas – the disadvantages of the former and the potential advantages of the latter. I also cover a price scoring formula that may assist in promoting fair working practices.
In this eUpdate, I further explore price scoring methodologies in light of detailed academic papers. My aim is to identify components formulas should ideally include (or not) in order to adhere to the Treaty principles of transparency and non-discrimination.
The time for doing so is opportune because the desire, or need, to be transparent seems to be gaining ground across the European Union. This is partly due to courts questioning the absurd results thrown up by some price scoring formulas. Also, to my knowledge, at least two member states have taken steps to further define good practice in price scoring:
- Portugal banned relative formulas in 2008 by decreeing that although mathematical formulas are permissible, scoring a price in a tender cannot be done by comparing it to other tenders; and
- France issued guidance to contracting authorities discouraging the use of formulas that, when applied, distort price differentials.
RELATIVE PRICE SCORING FORMULAS – FLAWS
The following “standard differential” example highlights an anomaly I have discussed previously, that despite the equal differences in prices between each bid (£5), Bidder 2 would find it more difficult to “catch up” Bidder 1 than Bidder 3 would to “catch up” Bidder 2. This is because, as we have seen, the formula penalises tenders that come closer to the most competitive price as opposed to tenders that are further from the most competitive price. The end result is that Bidder 2 may simply not be in the race through no fault of his own.

Bidder 1 bids £10 – 25% attributed
Bidder 2 bids £15 – 16.6% attributed (should be 18.75% to preserve price differences)
Bidder 3 bids £20 – 12.5% attributed (no adverse effect)
The above is an example of a “relative” pricing formula and illustrates why many analysts have concluded that relative price scoring formulas are perhaps best avoided.
So, how does one recognise a relative formula – or, better still, why should the “price differential” and the “average price” methods be avoided?
The quick answer is because tenderers know they will be measured against, or relative to, other bidders (“the lowest bid” or the “average” or “mean” price of all bids) but cannot know what that measure will be. Therefore, tenderers must make an assumption about what the measure will be in order to assess their own chances of achieving the maximum score.
There are of course many variations on relative scoring methods, for example:
- Giving a fixed percentage in accordance to each bid – so, 25% (or whatever the attributed split is) to the lowest; 23% to the second lowest price; 21% to the third lowest; etc. This has the flaw of failing to reflect, in any way, the actual differences between prices. The lowest price may be only £1 different from the second lowest, while the difference between second and third lowest could be £50 – thereby potentially penalising mid-ranking bids again.
- Giving a fixed percentage to bids within pre-determined ranges (defined by how far, in percentage terms, they are from the cheapest bid) – so, the lowest bid of £100 gets 25%; bids within 10% of £100 get 90% of the maximum score, i.e. 22.5%; bids within 20% of £100 get 80% of the maximum, i.e. 20%; etc. Again, this potentially fails to reflect the real difference, particularly if all bids are within 10% of each other – in that case, only two scores are given: 25% to the lowest bid and 22.5% to all other bids.
However, regardless of the method used, the tendering exercise can become non-transparent; and if the formula contains mathematical flaws or is non-linear, as illustrated above, using such formulas may also be discriminatory.
CAVEATS
However, to be fair, some caveats must be mentioned.
Price and quality split
I have assumed, for ease of consistency throughout all my eUpdates, a split of quality 75%, price 25%. It should be said that whilst contracting authorities are free to choose the split that suits them, courts have not shied away from questioning splits, for example a price weighted so highly that quality can be negated – to the extent that value for money is questionable (see Case T-461/08 Evropaiky Dynamiki – Proigmena Systimata Tilepikoinonion Pliroforikis kai Tilematikis AE v. European Investment Bank (BEI) [2011] ECR II-06367).
Only two bids?
The above formulas may work better when there are only 2 bids. That is because Bidder 2’s bid is where it is – in the second place. For example, in the standard differential model Bidder 2 cannot say that it should have obtained 18.75% as there are no other price differential to compare it with. Put differently, middle-ranking bids and wide divergence between different bids can only be penalised if such bids exist.
The problem of course is that contacting authorities are unlikely to know, at the time of setting the formula, how many bidders they will be assessing.
Minimal or small differences in prices?
Analysts have noted that the standard differential model could be used nevertheless when the differences in prices are minimal. That is because, although there is a distortion, “catching up” may not be “unsurmountable”. For example:
Bidder 1 bids £10 – 25% attributed
Bidder 2 bids £11 – 22.72% attributed (should be 22.91%, i.e Bid 1 25% less Bid 3 20.83% = 4.17%. The difference is then halved (2.08%) and then added to Bid 3 to reflect the price differentials).
Bidder 3 bids £12 – 20.83% attributed (no adverse effect)
The difference between each price is also equal (£1 instead of £5 as in our previous example). However, although it can be argued that Bidder 2 should have scored 22.91% (instead of 22.72%) to preserve the equal spacing in prices, bidder 2 is “only” being penalised to the tune of 0.19%.
Notwithstanding, the problem again is that contacting authorities may not know, at the time of setting the formula, what range in prices they will be assessing. In addition, when do bids become too “separated” in price to justify the use of the differential method?
Very high value contracts?
Again analysts have remarked that relative scoring formulas may be useful where contracts are of very high value. That said, I think it is more of a philosophical approach than a mathematical one.
The reasoning is that “attributing” percentages to very highly priced contracts is a better means with which to compare bids because the formula’s results make it easier to appreciate and comprehend the differential in prices.
That said, analysts stress the fact that the real issue is where the relative formula produces score differences that randomly disregards the respective competitiveness of the bids.
Contracting authorities dealing with contracts with very high financial values may therefore consider using relative formulas to assess prices and costs, but they should be aware that challenges may still arise as aggrieved contractors may argue lack of transparency, discrimination and unequal treatment.
PRICE SCORING FORMULAS – CAN WE DO BETTER?
Contracting authorities could seek to rely on formulas with an ideal price, from the contracting authorities’ point of view, set out in the Invitation to Tender (ITT). We have seen that the following model does have that element.
The formula is sometimes set out as follows:
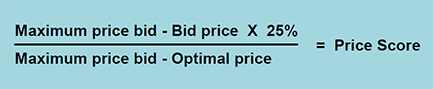
The above method works on the premise that the bid price closest to the optimal price gets the highest score whilst the maximum bid will score zero.
This method guards against abnormally low bids or against a “race to the bottom”. It also allows contracting authorities to test their ideal price against market place prices, and may take into account budget constraints or savings they wish to make etc.
However, tenderers are still to be measured against other bidders, being measured against “the maximum price bid”, and have to make an assumption about what that maximum might be.
That said, tenderers are in a better position because they know what the contracting authority is looking for – the optimum or ideal price is openly acknowledged at the outset.
PRICE SCORING FORMULAS – THE BEST ONES?
If one of the better formulas is the “optimum (or “fit to the budget”) pricing” method as seen above, are there variations to improve on it?
The formula can be as set out above but with a “maximum price” disclosed by the contracting authority beforehand in the same way as the contracting authorities’ “optimal price” is set out in advance. The maximum price is in effect simply an indication of what the contracting authorities are willing to pay – anything above being eliminated.
Also, in order to avoid any confusion, or to deal with vexatious tenders, contracting authorities may wish to state that no price below the ideal price will be accepted.
It must be pointed out that some academics have gone even further by introducing into this formula multipliers – for example a maximum price based on twice the ideal price.
This may be worth considering if only because this approach does not require bidders to make any assumptions about other tender prices, allowing them to score themselves before submitting their bids.
Lastly, it is fair to say that one may come up with a very rigorous mathematical formula, but doing so may introduce such complexities as to render the exercise non-transparent, the very thing we are trying to avoid.
THE HYBRID?
It may all sound rather complicated, so what about the formula I discarded (the price differential model) but slightly amended?
To explain, could we have:

In this way, we have an evaluation of each price assessed against the ideal price set by the contracting authority. The contracting authority is then also able to ensure that its “ideal price” comprises elements that may matter to it – for example the fair work practices and of course the Living Wage.
CONCLUSION
Pending the UK Government or the Scottish Government following Portugal’s and France’s examples, and UK courts following courts’ rulings in other member states to address and deal with the issues I have explored, it is left to contracting authorities to adopt the formula or formulas that suit them best in the context of what they are procuring.
However, rather than search, in vain perhaps, for the ideal all singing and dancing price scoring formula, perhaps we can identify which elements or components of a formula should be avoided and which should be considered and if suitable adopted:
- Avoid formulas that have non-linear functions, i.e. formulas that are disproportionately “degressive”.
- Do not assess a bid exclusively in accordance with other competing bids. Assess it instead in accordance with its intrinsic value – in other words, consider absolute price scoring formulas.
- If a maximum score is to be allocated to the best price, with some bids allocated a score of zero (or minus), that this be done within stated parameters, i.e. contracting authorities defining exactly, price-range wise, what will be acceptable and what will not.
Notwithstanding the above, or my previous articles on price scoring, having analysed a number of pricing formulas with a view to identifying which are less likely to cause concern, another area to address is the relation that exists between quality assessment and price scoring (or assessment). The basis on which quality “and” price should be assessed in order to achieve the most economically advantageous tender (MEAT) is also important to consider.
This is particularly relevant in Scotland, where the Public Contracts (Scotland) Regulations 2015 now require that prices should never be considered in isolation.
To that end I will explore what MEAT is as well as the matter of quality / price ratios in my next eUpdate.
If you have any questions in relation to procurement, and this topic in particular, please do not hesitate to contact BTO on 0141 221 8012.
Look out for my next eUpdate in this series on “Tender evaluations, MEAT and ratios”
Sources and Acknowledgements
“La question de la régularité de la méthode proportionnelle d’évaluation du critère du prix.” Etude par Pascal MOREAU doctorant en droit pubic à l’université de Poitiers - capitaine de police chargé d’enquêtes en matière de corruption en marchés publics. (12, Décembre 2014, etude 11).
Links to previous eUpdates:
Price Scoring - Getting it wrong?
Price Scoring, Fair Work Practices...and the Living Wage


